Calibration for Decision Making: A Principled Approach to Trustworthy ML

 Over on the Let-All blog, Georgy Noarov and I wrote post on calibration through the lens of decision making. We think calibration has strong semantics as "trustworthiness", and that lots can be gained by designing uncertainty quantification for particular decision making tasks.

You can read the post here: https://www.let-all.com/blog/2024/03/13/calibration-for-decision-making-a-principled-approach-to-trustworthy-ml/

Batch Multivalid Conformal Prediction

 

Our new paper gives very simple algorithms that promise "multivalid" conformal prediction sets for exchangable data. This means they are valid not just marginally, but also conditionally on (intersecting!) group membership, and in a threshold calibrated manner. I'll explain!

Instead of making point predictions, we can quantify uncertainty by producing "prediction sets" --- sets of labels that contain the true label with (say) 90% probability. The problem is, in a k label prediction problem, there are $2^k$ prediction sets. The curse of dimensionality!

One of the great ideas of conformal prediction is that if we can find a good "non-conformity score" s(x,y) telling us how unusual a label y seems for features x, we can focus on a 1-parameter family of prediction sets $P(x, t) = \{y : s(x,y) < t\}$. Now the problem is just to find $t$.

The usual recipe in split conformal prediction is to use a holdout set of points (x,y) to find a $t$ such that $\Pr[s(x,y) \leq t] = 0.9$. Then over the randomness of new examples (x,y), we have that $\Pr[y \in P(x,t)] = 0.9$. This is a -marginal- guarantee: the randomness is over x and y.

 

Suppose we have a bunch of groups (subsets of the feature space) g that we think are prediction-relevant? g could record e.g. demographic or other attributes of people. We might want to promise $\Pr[y \in P(x,t) | x \in g] = 0.9$. Vanilla split conformal doesn't promise this. 

 

If the groups g are disjoint, you could use a different threshold $t_g$ for each group --- but what if a single example can be a member of multiple groups? You can be conservative and use the largest threshold $t_g$ among all groups g that x is a member of, but this will over-cover.

 

The first insight here is that it no longer suffices to find a single threshold $t$ --- we need to find a function f mapping examples to thresholds, and to consider prediction sets $P(x,f(x)) =\{y : s(x,y) < f(x)\}$. The problem is to use a calibration set to train the function f. 

 

Our first algorithm is super simple and given any set of (intersecting!) groups G, trains f such that for every $g \in G$, we have that for new examples, $\Pr[y \in P(x,f(x))|g\in G] = 0.9$. How? f just minimizes pinball loss over linear combinations of group indicator functions $g \in G$. 

Now that we are using different thresholds f(x) for different x, you might worry that the threshold f(x) itself is correlated with coverage. To make sure its not, we can also ask for threshold calibration: $\Pr[y \in P(x,f(x)) | x \in g, f(x) = t] = 0.9$ for all $g \in G$ and all t. 

Our second algorithm trains f so that it has both group conditional and threshold calibrated coverage - what we call "full multivalid" coverage. It is also simple: It iteratively finds pairs $(g,t)$ on which multivalid coverage is violated empirically, and corrects the violations. 

 

This is the batch analogue of what we did in our NeurIPS 2022 paper in the sequential setting, which I wrote about here:  https://aaronsadventures.blogspot.com/2022/06/practical-robust-and-equitable.html The sequential setting is more difficult in many respects (no need to assume exchangable data!) but it requires labels at test time. Our new algorithms don't.

Both algorithms are very performant, taking a couple of seconds to train on thousands of points. Our first algorithm gets nearly perfect group conditional coverage on real datasets, and our second is never off by more than 1%, both improving significantly on baselines.

 

Our second algorithm gets better threshold calibration than our first (and compared to baselines), as expected. But perhaps surprisingly, our first algorithm performs quite well on calibration tests --- significantly beating baselines --- despite no formal calibration guarantees.

 

Our techniques come from the algorithmic fairness literature --- we train f to satisfy quantile analogues of multicalibration and multi-accuracy. If you haven't been paying attention to algorithmic fairness, maybe you should start --- there is interesting stuff going on there! Check out e.g. the Simons Collaboration on Algorithmic Fairness

This is joint work with the excellent Chris Jung, Georgy Noarov, and Ramya Ramalingam.

Our paper is here: https://arxiv.org/abs/2209.15145 and our code is here: https://github.com/ProgBelarus/BatchMultivalidConformal

 

Practical, Robust, and Equitable Uncertainty Estimation

This is a post about a new paper that is joint work with Bastani, Gupta, Jung, Noarov, and Ramalingam. The paper is here: https://arxiv.org/abs/2206.01067 and here is a recording of a recent talk I gave about it at the Simons Foundation: https://www.simonsfoundation.org/event/robust-and-equitable-uncertainty-estimation/ . This is cross-posted to the TOC4Fairness Blog (and this work comes out of the Simons Collaboration on the Theory of Algorithmic Fairness)

Machine Learning is really good at making point predictions --- but it sometimes makes mistakes. How should we think about which predictions we should trust? In other words, what is the right way to think about the uncertainty of particular predictions? Together with Osbert Bastani, Varun Gupta, Chris Jung, Georgy Noarov, and Ramya Ramalingam, we have some new work I'm really excited about. 

A natural way to quantify uncertainty is to predict a set of labels rather than a single one. Pick a degree of certainty --- say 90%. For every prediction we make, we'd like to return the smallest set of labels that is guaranteed to contain the true label 90% of the time. These are "prediction sets", and quantify uncertainty in a natural way: ideally, we will be sure about the correct label, and the prediction set will contain only a single label (the prediction we are certain about). But the larger our prediction set, the more our uncertainty, and the contents of the prediction set lets us know what exactly the model is uncertain about. 

An example of prediction sets for ImageNet. This example comes from a nice recent paper by Angelopoulos, Bates, Malik, and Jordan: https://arxiv.org/abs/2009.14193 

But how can we do this? Conformal Prediction provides a particularly simple way. Here is an outline of the vanilla version of conformal prediction (there are plenty of variants): 

Step 1: Pick a (non)conformity score to measure how different a label y is from a prediction f(x). e.g. for a regression model we could choose $s(x,y) = |f(x)-y|$ --- but lots of interesting work has been done recently to develop much fancier ones. A lot of the art of conformal prediction is in finding a good score function.

Step 2: Find a threshold $\tau$ such that for a new example $(x,y)$, $\Pr[s(x,y) \leq \tau] = 0.9$. An easy way to do this is using a holdout set. 

Step 3: On a new example $x$, given a point prediction $f(x)$, produce the prediction set $P(x) = \{y : s(x,y) \leq \tau\}$. 

Thats it! Nice and simple. Check out this recent survey by Angelopolous and Bates for an accessible introduction to conformal prediction. 

But a few things could go wrong. First, the technique of using a holdout set only works if the data is i.i.d. or more generally exchangable --- i.e. the data distribution should be permutation invariant. But maybe its coming from some changing distribution. If the distribution has changed in an expected and well behaved way, there are some fixes that let you apply the same framework, but if not you are likely in trouble.

A joke about non-exchangable data

Second, an average over everyone might not be what you care about. If we are in a personalized medicine setting, you might care about the reliability of predictions not just overall, but for women with a family history of diabetes and egg allergies --- or whatever else you think is medically relevant about you as an individual.

This is the problem that we want to solve: How to give prediction sets that cover their label 90% of the time even if we make no assumptions at all about the data generating process, and even if we care about coverage conditional on arbitrary intersecting subsets of the data.

We want stronger guarantees in another way too. If you think about our goal, there is a way to cheat: 90% of the time, predict the (trivial) set of all labels. 10% of the time predict the empty set. This covers the real label 90% of the time, but is completely uninformative.

To avoid this "solution", we also ask that our predictions be threshold calibrated. Remember our prediction sets have the form $P_t(x) = \{y : s(x,y) \leq \tau_t\}$. Now the threshold $\tau_t$ might be different every day. But we want 90% coverage even conditional on the value of $\tau_t$.

This rules out cheating. Remarkably (I think!), for every set of groups specified ahead of time, we're able to guarantee that even if the data is generated by an adversary, that our empirical coverage converges to 90% at the statistically optimal rate. Here is what that means:

Pick a threshold $\tau$ and group $G$. Consider all $n_{\tau,G}$ rounds in which the example $x$ was in $G$, and in which we predicted threshold $\tau$.  We promise that on this set, we cover 90% $\pm$ $1/\sqrt{n_{\tau,G}}$ of the labels. This is the best you could do even with a known distribution.

The best thing is that the algorithm is super simple and practical. We had a paper last year that showed how to do much of this in theory --- but the algorithm from that paper was not easily implementable (it involved solving an exponentially large linear program with a separation oracle).  But here is our new algorithm --- it only involves doing a small amount of arithmetic for each prediction:

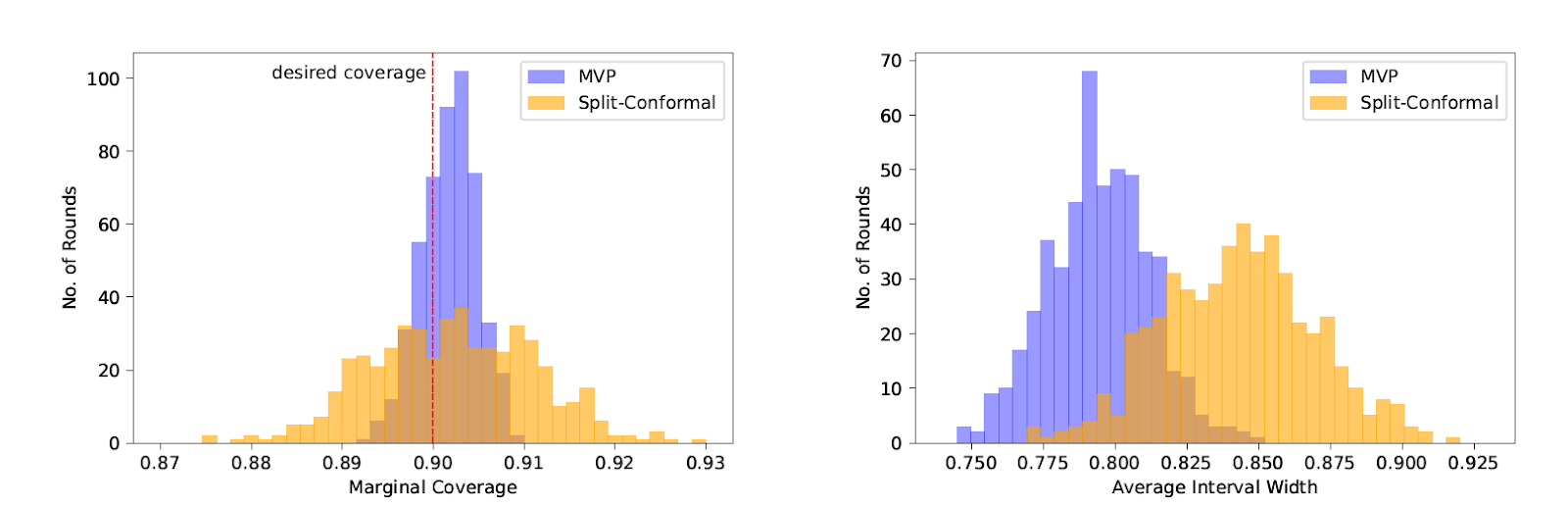
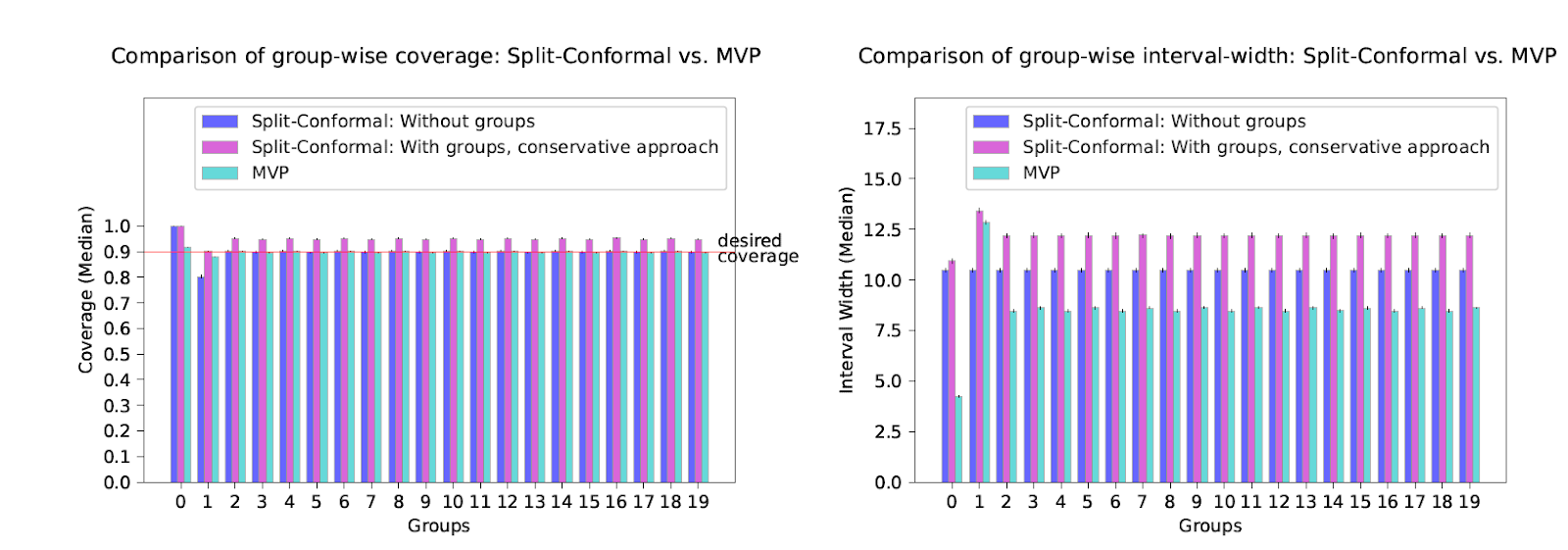
So we're able to implement it and run a bunch of experiments. You can read about them in detail in the paper, but the upshot is that our new method is competitive with split conformal prediction even on "its own turf" --- i.e. when the data really is drawn i.i.d. and we only care about marginal coverage --- and really excels when the data comes from a more complicated source, or when we measure group-conditional coverage, which traditional methods tend to have much more trouble with. We run experiments on regression and classification tasks, on exchangeable data, under distribution shift, on real time series data, and on adversarial data orderings. Even when the data is i.i.d. and we only care about marginal coverage, our method has an important advantage over split conformal prediction --- since we don't need to preserve exchangability, we can use all of the data to train the underlying model, whereas split conformal prediction needs to reserve some fraction of it for a holdout set. The result is faster learning for our method, which results in smaller/more accurate prediction sets even without the complicating factors of groupwise coverage, threshold calibration or adversarial data!

FORC 2021 Call for Papers

 Reminder to anyone who has forgotten about FORC 2021 --- its a very nice venue --- and also a nice place to highlight recent work that is published or submitted elsewhere, via the non-archival track.

Symposium on Foundations of Responsible Computing (FORC) 2021 Call for Papers - Deadline February 15, 2021 AOE (anywhere on Earth)

The second annual Symposium on Foundations of Responsible Computing (FORC) is planned to be held on June 9-11, 2021, *online*. FORC is a forum for mathematically rigorous research in computation and society writ large.  The Symposium aims to catalyze the formation of a community supportive of the application of theoretical computer science, statistics, economics, and other relevant analytical fields to problems of pressing and anticipated societal concern.

Topics that fall in scope include, but are not restricted to, formal approaches to privacy, including differential privacy; theoretical approaches to fairness in machine learning, including the investigation of definitions, algorithms and lower bounds, tradeoffs, and economic incentives; computational and mathematical social choice (including apportionment and redistricting); theoretical foundations of sustainability; mechanism design for social good; mathematical approaches to bridging computer science, law and ethics; and theory related to modeling and mitigating the spread of epidemics. The Program Committee also warmly welcomes mathematically rigorous work on societal problems that have not traditionally received attention in the theoretical computer science literature. Whatever the topic, submitted papers should communicate their contributions towards responsible computing, broadly construed.

The symposium itself will feature a mixture of talks by authors of accepted papers and invited talks. At least one author of each accepted paper should be present at the symposium to present the work (with an option for virtual attendance, as needed).

Dual Submission Policy. Authors must indicate at the time of submission whether they are submitting to the archival-option track or the non-archival track.

* For submissions to the non-archival track, it is permitted to submit papers that have appeared in a peer-reviewed conference or journal since the last FORC. It is also permitted to simultaneously or subsequently submit substantially similar work to another conference or to a journal. Accepted papers in the non-archival track will receive talks at the symposium and will appear as one-page abstracts on the symposium website. They will not appear in the proceedings.

* For submissions to the archival-option track, papers that are substantially similar to papers that have been previously published, accepted for publication, or submitted in parallel to other peer-reviewed conferences with proceedings may not be submitted. Also, submissions that are substantially similar to papers that are already published in a journal at the time of submission may not be submitted to the archival-option track. Accepted papers in the archival-option track will receive talks at the symposium. Authors of papers accepted to the archival-option track will be given the option to choose whether to convert to a one-page abstract (which will not appear in the proceedings) or publish a 10-page version of their paper in the proceedings. The proceedings of FORC 2021 will be published by LIPIcs.

Authors are also responsible for ensuring that submitting to FORC would not be in violation of other journals’ or conferences’ submission policies.

PC members and reviewers will be aware during the review process of whether papers have been submitted as archival-option or non-archival. The PC reserves the right to hold non-archival papers to a different standard than archival-option papers.

Submission Instructions.
* Authors should upload a PDF of the paper here: https://easychair.org/conferences/?conf=forc2021.
* A footnote on the title of the paper should indicate whether the paper is a submission to the archival-option track or the non-archival track. Submissions to the non-archival track should also indicate in this footnote any archival venues (conferences or journals) at which the paper has appeared, a link to the publication, and the date on which it was published.
* The font size should be at least 11 point and the format should be single-column.
* Author names and affiliations should appear at the top of the paper (reviewing for FORC is single, not double blind).
* Beyond these, there are no formatting or length requirements, but reviewers will only be asked to read the first 10 pages of the submission. It is the authors’ responsibility that the main results of the paper and their significance be clearly stated within the first 10 pages. For both the archival-option track and the non-archival track, submissions should include proofs of all central claims, and the committee will put a premium on writing that conveys clearly and in the simplest possible way what the paper is accomplishing.
* Authors are free to post their submissions on arXiv or other online repositories.


All questions about submissions should be emailed to the PC chair, Katrina Ligett, at katrina@cs.huji.ac.il

FORC Steering Committee

Avrim Blum
Cynthia Dwork      
Shafi Goldwasser  
Sampath Kannan
Jon Kleinberg
Kobbi Nissim  
Toni Pitassi
Omer Reingold
Guy Rothblum  
Salvatore Ruggieri
Salil Vadhan
Adrian Weller


FORC 2021 Program Committee

Borja Balle
Raef Bassily
Mark Bun
Elisa Celis
Aloni Cohen
Moon Duchin
Vitaly Feldman
Kira Goldner
Krishna Gummadi
Swati Gupta
Gautam Kamath
Michael Kearns
Scott Kominers
Himabindu Lakkaraju
Katrina Ligett (chair)
Jamie Morgenstern
Seth Neel
Kobbi Nissim
Adam Smith
Kunal Talwar
Salil Vadhan

Important Dates

Submission deadline: February 15, 2021 AOE (anywhere on Earth)
Author notification: March 31, 2021
Conference: June 9-11, 2021

How to Estimate the Uncertainty of Predictions

This is a post about a new paper Online Multivalid Learning: Means, Moments, and Prediction Intervals, that is joint work with Varun Gupta, Christopher Jung, Georgy Noarov, and Mallesh Pai. It is cross-posted to the new TOC4Fairness blog. For those that prefer watching to reading, here is a recording of a talk I gave on this paper. 

Suppose you go and train the latest, greatest machine learning architecture to predict something important. Say (to pick an example entirely out of thin air) you are in the midst of a pandemic, and want to predict the severity of patients' symptoms in 2 days time, so as to triage scarce medical resources. Since you will be using these predictions to make decisions, you would like them to be accurate in various ways: for example, at the very least, you will want your predictions to be calibrated, and you may also want to be able to accurately quantify the uncertainty of your predictions (say with 95% prediction intervals). It is a fast moving situation, and data is coming in dynamically --- and you need to make decisions as you go. What can you do?

The first thing you might do is ask on twitter! What you will find is that the standard tool for quantifying uncertainty in settings like this is conformal prediction. The conformal prediction literature has a number of elegant techniques for endowing arbitrary point prediction methods with marginal prediction intervals: i.e intervals $(\ell(x), u(x))$ such that over the randomness of some data distribution over labelled examples $(x,y)$: $\Pr_{(x,y)}\left[y \in [\ell(x), u(x)]\right] \approx 0.95$ These would be 95% marginal prediction intervals --- but in general you could pick your favorite coverage probability $1-\delta$.

Conformal prediction has a lot going for it --- its tools are very general and flexible, and lead to practical algorithms. But it also has two well known shortcomings:

1. Strong Assumptions. Like many tools from statistics and machine learning, conformal prediction methods require that the future look like the past. In particular, they require that the data be drawn i.i.d. from some distribution --- or at least be exchangable (i.e. their distribution should be invariant to permutation). This is sometimes the case --- but it often is not. In our pandemic scenario, the distribution on patient features might quickly change in unexpected ways as the disease moves between different populations, as might the relationship between features and outcomes, as treatments advance. In other settings in which consequential decisions are being made about people --- like lending and hiring decisions --- people might intentionally manipulate their features in response to the predictive algorithms you deploy, in an attempt to get the outcome they want. Or you might be trying to predict outcomes in time series data, in which there are explicit dependencies across time. In all of these scenarios, exchangeability is violated.
2. Weak Guarantees. Marginal coverage guarantees are averages over people. 95% marginal coverage means that the true label falls within the predicted interval for 95% of people. It need not mean anything for people like you. For example, if you are part of a demographic group that makes up less than 5% of the population, it is entirely consistent with the guarantees of a 95% marginal prediction interval that labels for people from your demographic group fall outside of their intervals 100% of the time. This can be both an accuracy and a fairness concern --- marginal prediction works well for "typical" members of a population, but not necessarily for everyone else.

What kinds of improvements might we hope for? Lets start with how to strengthen the guarantee:

Multivalidity Ideally, we would want conditional guarantees --- i.e. the promise that for every $x$, that we would have $\Pr_{y}\left[y \in [\ell(x), u(x)] | x \right] \approx 0.95$. In other words, that somehow for each individual, the prediction interval was valid for them specifically, over the "unrealized" (or unmeasured) randomness of the world. Of course this is too much to hope for. In a rich feature space, we have likely never seen anyone exactly like you before (i.e. with your feature vector $x$). So strictly speaking, we have no information at all about your conditional label distribution. We still have to average over people. But we don't have to average over everybody. An important idea that has been investigated in several different contexts in recent years in the theory literature on fairness is that we might articulate a very rich collection of (generally intersecting) demographic groups $G$ corresponding to relevant subsets of the data domain, and ask for things that we care about to hold true as averaged over any group $S \in G$ in the collection. In the case of prediction intervals, this would correspond to asking for something like that simultaneously for every demographic group $S \in G$, $\Pr_{(x,y)}\left[y \in [\ell(x), u(x)] | x \in S \right] \approx 0.95$. Note here that an individual might be a member of many different demographic groups, and can interpret the guarantees of their prediction interval as averages over any of those demographic groups, at their option. This is what we can achieve --- at least for any such group that isn't too small. 

And what kinds of assumptions do we need?

Adversarial Data Actually, its not clear that we need any! Many learning problems which initially appear to require distributional assumptions turn out to be solvable even in the worst case over data sequences --- i.e. even if a clever adversary, with full knowledge of your algorithm, and with the intent only to sabotage your learning guarantees, is allowed to adaptively choose data to present to your algorithm. This is the case for calibrated weather prediction, as well as general contextual prediction. It turns out to be the case for us as well. Instead of promising coverage probabilities of $1-\delta + O(1/T)$ after $T$ rounds on the underlying distribution, as conformal prediction is able to, (for us there is no underlying distribution) we offer empirical coverage rates of $1-\delta \pm O(1/\sqrt{T})$. This kind of guarantee is quite similar to what conformal prediction guarantees about empirical coverage.

More Generally Our techniques are not specific to prediction intervals. We can do the same thing for predicting label means, and predicting variances of the residuals of arbitrary prediction methods. For mean prediction, this corresponds to an algorithm for providing multi-calibrated predictions in the sense of Hebert-Johnson et al, in an online adversarial environment. For variances and other higher moments, it corresponds to an online algorithm for making mean-conditioned moment multicalibrated predictions in the sense of Jung et al.

Techniques At the risk of boring my one stubbornly remaining reader, let me say a few words about how we do it. We generalize an idea that dates back to an argument that Fudenberg and Levine first made in 1995 --- and is closely related to an earlier, beautiful argument by Sergiu Hart --- but that I just learned about this summer, and thought was just amazing. It applies broadly to solving any prediction task that would be easy, if only you were facing a known data distribution. This is the case for us. If, for each arriving patient at our hospital, a wizard told us their "true" distribution over outcome severity, we could easily make calibrated predictions by always predicting the mean of this distribution --- and we could similarly read off correct 95% coverage intervals from the CDF of the distribution. So what? That's not the situation we are in, of course. Absent a wizard, we first need to commit to some learning algorithm, and only then will the adversary decide what data to show us.

But lets put our game theory hats on. Suppose we've been making predictions for awhile. We can write down some measure of our error so far --- say the maximum, over all demographic groups in $G$, of the deviation of our empirical coverage so far from our 95% coverage target. For the next round, define a zero sum game, in which we (the learner) want to minimize the increase in this measure of error, and the adversary wants to maximize it. The defining feature of zero-sum games is that how well you can do in them is independent of which player has to announce their distribution on play first --- this is the celebrated Minimax Theorem. So to evaluate how well the learner could do in this game, we can think about the situation involving a Wizard above, in which for each arriving person, before we have to make a prediction for them, we get to observe their true label distribution. Of course in this scenario we can do well, because for all of our goals, our measure of success is based on how well our predictions match observed properties of these distributions. The Minimax theorem tells us that (at least in principle --- it doesn't give us the algorithm), there must therefore also be a learning algorithm that can do just as well, but against an adversary.

The minimax argument is slick, but non-constructive. To actually pin down a concrete algorithm, we need to solve for the equilibrium in the corresponding game. That's what we spend much of the paper doing, for each of the prediction tasks that we study. For multicalibration, we get a simple, elementary algorithm --- but for the prediction interval problem, although we get a polynomial time algorithm, it involves solving a linear program with a separation oracle at each round. Finding more efficient and practical ways to do this strikes me as an important problem.

Finally, I had more fun writing this paper --- learning about old techniques from the game theoretic calibration literature --- than I've had in awhile. I hope a few people enjoy reading it!

 

No Regret Algorithms from the Min Max Theorem

The existence of no-regret learning algorithms can be used to prove Von-Neumann's min-max theorem. This argument is originally due to Freund and Schapire, and I teach it to my undergraduates in my algorithmic game theory class. The min-max theorem also can be used to prove the existence of no-regret learning algorithms. Here is a constructive version of the argument (Constructive in that in the resulting algorithm, you only need to solve polynomially sized zero-sum games, so you can do it via linear programming).

Recall the setting. Play proceeds in rounds $t \in \{1,\ldots,T\}$. At each day $t$, the learner chooses one of $k$ actions $i_t \in \{1,\ldots,k\}$, and the adversary chooses a loss vector $\ell^t \in [0,1]^k$. The learner incurs loss $\ell^t_{i_t}$, corresponding to the action he chose. At the end of the interaction, the regret of the learner is defined to be the difference between the cumulative loss he incurred and the cumulative loss of the best fixed action (played consistently)  in hindsight:

$$\textrm{Regret}_T = \max_j \left(\sum_{t=1}^T \ell^t_{i_t} - \ell^t_j\right)$$ 

A classical and remarkable result is that there exist algorithms that can guarantee that regret grows only sublinearly with time: $\textrm{Regret}_T = O(\sqrt{T})$. Lets prove this. 

Define the non-negative portion of our cumulative regret with respect to action $j$ up until day $d$ as:

$$V_d^j = \left(\sum_{t=1}^d\left(\ell^t_{i_t} - \ell^t_j\right)\right)^+$$

and our additional regret at day $d+1$ with respect to action $j$ as:

$$r_{j}^{d+1} = \ell_{i_{d+1}}^{d+1} - \ell^{d+1}_j$$

Observe that if $V_{d}^j \geq 1$  then $V_{d+1}^j = V_d^j + r_j^{d+1}$. 

Define a surrogate loss function as our squared cumulative regrets, summed over all actions: 

$$L_d = \sum_{j=1}^k (V_d^j)^2$$

Observe that we can write the expected gain in our loss on day $d+1$, conditioned on the history thus far:

$$\mathbb{E}[L_{d+1} - L_d] \leq \sum_{j : V_d^j \geq 1} \mathbb{E}[(V_d^j+r_j^{d+1})^2 - (V_d^j)^2) ] + 3k$$

$$= \sum_{j : V_d^j \geq 1} \left(2V_d^j \mathbb{E}[r_{j}^{d+1}] + \mathbb{E}[(r_{j}^{d+1})^2]\right) + 3k $$

$$\leq \sum_{j=1}^k \left(2V_d^j \mathbb{E}[r_{j}^{d+1}]\right) + 4k$$

where the expectations are taken over the randomness of both the learner and the adversary in round $d+1$. 

Now consider a zero-sum game played between the learner and the adversary in which the learner is the minimization player, the adversary is the maximization player, and the utility function is $$u(i_{d+1}, \ell^{d+1}) = \sum_{j=1}^k \left(2V_d^j \mathbb{E}[r_{j}^{d+1}]\right)$$ The min-max theorem says that the learner can guarantee the same payoff for herself in the following two scenarios:

1. The learner first has to commit to playing a distribution $p_{d+1}$ over actions $i$, and then the adversary gets to best respond by picking the worst possible loss vectors, or
2. The adversary has to first commit to a distribution over loss vectors $\ell$ and then the learner gets the benefit of picking the best action $i_{d+1}$ to respond with. 

Scenario 1) is the scenario our learner finds herself in, when playing against an adaptive adversary. But 2) is much easier to analyze. If the adversary first commits to a distribution over loss vectors $\ell^{d+1}$, the learner can always choose action $i_{d+1} = \arg\min_j \mathbb{E}[\ell^{d+1}_j]$, which guarantees that $\mathbb{E}[r_{j}^{d+1}] \leq 0$, which in turn guarantees that the value of the game $ \sum_{j=1}^k \left(2V_d^j \mathbb{E}[r_{j}^{d+1}]\right) \leq 0$.  Hence, the min-max theorem tells us that the learner always has a distribution over actions $p_{d+1}$ that guarantees that $\mathbb{E}[L_{d+1} - L_d] \leq 4k$, even in the worst case over loss functions. If the learner always plays according to this distribution, then by a telescoping sum, we have that:

$$\mathbb{E}[L_T] \leq 4kT$$.

We therefore have by Jensen's inequality that:

$$\mathbb{E}[\max_j (V^j_T)] \leq \sqrt{\mathbb{E}[\max_j (V^j_T)^2]}\leq \sqrt{\mathbb{E}[\sum_{j=1}^k (V_j^T)^2]} \leq 2\sqrt{kT}$$.

Moment Multicalibration for Uncertainty Estimation

This blog post is about a new paper that I'm excited about, which is joint work with Chris Jung, Changhwa Lee, Mallesh Pai, and Ricky Vohra. If you prefer watching talks, you can watch one I gave to the Wharton statistics department here.

Suppose you are diagnosed with hypertension, and your doctor recommends that you take a certain drug to lower your blood pressure. The latest research, she tells you, finds that the drug lowers diastolic blood pressure by an average of 10 mm Hg. You remember your statistics class from college, and so you ask about confidence intervals. She looks up the paper, and tells you that it reports a 95% confidence interval of [5, 15]. How should you interpret this? 

What you might naively hope is that [5, 15] represents a conditional prediction interval. If you have some set of observable features $x$, and a label $y$ (in this case corresponding to your decrease in diastolic blood pressure after taking the drug), a 95% conditional prediction interval would promise that:

$$\Pr_y [y \in [5, 15] | x] \geq 0.95$$

In other words, a conditional prediction interval would promise that given all of your observed features, over the unrealized/unmeasured randomness of the world, there is a 95% chance that your diastolic blood pressure will decrease by between 5 and 15 points. 

But if you think about it, coming up with a conditional prediction interval is essentially impossible in a rich feature space. If $x$ contains lots of information about you, then probably there was nobody in the original study population that exactly matched your set of features $x$, and so we have no information at all about the conditional distribution on $y$ given $x$ --- i.e. no samples at all from the distribution over which our coverage probability supposedly holds! So how can you expect any sort of promise at all? There are two typical ways around this difficulty. 

The first is to make heroic assumptions about the data generation process. For example, if we assume that the world looks like an ordinary least squares model, and that there is a linear relationship between $y$ and $x$, then we can form a confidence region around the parameters of the model, and from that derive prediction intervals. But these prediction intervals are not valid if the model fails to hold, which it inevitably will. 

The second is to give up on conditional prediction intervals, and instead give marginal prediction intervals. This is what the conformal prediction literature aims to do. A marginal prediction interval looks quite similar to a conditional prediction interval (at least syntactically), and promises:

$$\Pr_{(x,y)} [y \in [5, 15] ] \geq 0.95$$

Rather than conditioning on your features $x$, a marginal prediction interval averages over all people, and promises that 95% of people who take the drug have their diastolic blood pressure lowered by between 5 and 15 points. But the semantics of this promise are quite different than that of a conditional prediction interval. Because the average is now taken over a large, heterogeneous population, very little is promised to you. For example, it might be that for patients in your demographic group (e.g. middle aged women with Sephardic Jewish ancestry and a family history of diabetes) that the drug is actually expected to raise blood pressure rather than lower it. Because this subgroup represents less than 5% of the population, it is entirely consistent with the marginal prediction interval being correct. Of course, if you are lucky, then perhaps someone has conducted a study of people from this demographic group and has computed marginal prediction intervals over it! But what if there are multiple different groups that you are a member of, over which the results seem to conflict? For example, you might also have a low BMI value and have unusually good cholesterol readings --- features of a group for which the drug works unusually well. Which uncertainty estimate should you trust, if you are a member of both groups? 

These concerns actually arise already when we think about the semantics of mean estimations ("the expected drop in blood pressure amongst patients who take this drug is 10 mm Hg"). Ideally, if you were a patient with features $x$, then 10 would be an estimate of $\mathbb{E}[y | x]$. But just as with uncertainty estimation, in a large feature space, we typically have no information about the distribution on $y$ conditional on $x$ (because we have never met anyone exactly like you before), and so instead what we have is just an estimate of $\mathbb{E}[y]$ --- i.e. averaging over people. If you have a method of making predictions $f(x)$ as a function of features $x$, then a standard performance metric is calibration --- which informally asks that for every prediction $p$, amongst all people for whom we predicted $f(x) = p$, the average of the realized labels $y$ should be $p$. Again, estimates of this form promise little to individuals, because they are averages over a large and heterogeneous population.   

Several years ago, Hebert-Johnson et al. proposed a nice way to interpolate between the (impossible) ideal of offering conditional mean predictions  $f(x) = \mathbb{E}[y | x]$, and the weak guarantee of merely offering calibrated predictions $f$. Roughly speaking, they proposed to specify a very large collection of potentially intersecting groups $G$ (representing e.g. demographic groups like Sephardic Jewish women with a family history of diabetes, and hypertensive patients with low cholesterol and BMI values, etc) and to ask that a trained predictor be simultaniously calibrated on each sufficiently large group in $G$. They showed how to accomplish this using a polynomially sized sample from the underlying distribution, with polynomial running time overhead, on top of the cost of solving learning problems over $G$. 

In our paper, we --- roughly speaking --- show how to accomplish the same thing, but for variances and other higher moments, in addition to just means. And our "multicalibrated moment estimates" can be used to construct prediction intervals in exactly the same way that real moments of the conditional label distribution could be used. If you used the real (unknown) label distribution moments, you would have gotten conditional prediction intervals. If you use our multi-calibrated moments, you get marginal prediction intervals that are simultaneously valid as averaged over each of the groups in $G$. So, for example, our hypertensive patient above could interpret her prediction interval --- if it was constructed from multicalibrated moment estimates computed from her features --- as an average over each of the demographic groups that she is a member of (so long as they are contained within $G$), and all of those interpretations would be simultaneously valid. 

I'll leave the details to the paper --- including what exactly we mean by "moment multicalibration". I'll just note that a major difficulty is that variances and higher moments --- unlike expectations --- do not combine linearly, so it is no longer sensible to ask that "amongst all people for whom we predicted variance v, the true variance should be v" --- because even the true conditional label variances do not satisfy this property. But it is sensible to ask that a pair of mean and moment predictions be calibrated in this way: "amongst all people for whom we predicted mean $\mu$ and variance v, the true mean should be $\mu$ and the true variance should be $v$." This is what we call "mean-conditioned moment calibration", and it is satisfied by the true distributional moments. 

The paper is here: Moment Multicalibration for Uncertainty Estimation.