I've been having fun recently reading about "AI Risk". There is lots of eloquent writing out there about this topic: I especially recommend
Scott Alexander's Superintelligence FAQ for those looking for a fun read. The subject has reached the public consciousness, with high profile people like
Stephen Hawking and
Elon Musk speaking publicly about it. There is also an increasing amount of funding and research effort being devoted to understanding AI risk. See for example the
Future of Humanity Institute at Oxford, the
Future of Life Institute at MIT, and the
Machine Intelligence Research Institute in Berkeley, among others. These groups seem to be doing lots of interesting research, which I am mostly ignorant of. In this post I just want to talk about a simple exercise in asymptotics.
First, Some Background.
A "superintelligent" AI is loosely defined to be an entity that is much better than we are at essentially any cognitive/learning/planning task. Perhaps, by analogy, a superintelligent AI is to human beings as human beings are to Bengal tigers, in terms of general intelligence. It shouldn't be hard to convince yourself that if we were in the company of a superintelligence, then we would be very right to be worried: after all, it is intelligence that allows human beings to totally dominate the world and drive Bengal tigers to near extinction, despite the fact that tigers physiologically dominate humans in most other respects. This is the case even if the superintelligence doesn't have the destruction of humanity as a goal per-se (after all, we don't have it out for tigers), and even if the superintelligence is just an unconscious but super-powerful optimization algorithm. I won't rehash the arguments here (
Scott does it better) but it essentially boils down to the fact that it is quite hard to anticipate what the results of optimizing an objective function will be, if the optimization is done over a sufficiently rich space of strategies. And if we get it wrong, and the optimization has some severely unpleasant side-effects? It is tempting to suggest that at that point, we just unplug the computer and start over. The problem is that if we unplug the intelligence, it won't do as well at optimizing its objective function compared to if it took steps to prevent us from unplugging it. So if it's strategy space is rich enough so that it is able to take steps to defend itself, it will. Lots of the most interesting research in this field seems to be about how to align optimization objectives with our own desires, or simply how to write down objective functions that don't induce the optimization algorithm to try and prevent us from unplugging it, while also not incentivizing the algorithm to unplug itself (the
corrigibility problem).
Ok. It seems uncontroversial that a hypothetical superintelligence would be something we should take very seriously as a danger. But isn't it premature to worry about this, given how far off it seems to be? We aren't even that good at
making product recommendations, let alone optimization algorithms so powerful that they might inadvertently destroy all of humanity. Even if superintelligence will ultimately be something to take very seriously, are we even in a position to productively think about it now, given how little we know about how such a thing might work at a technical level? This seems to be the position that Andrew Ng was taking, in his much quoted statement that (paraphrasing) worrying about the dangers of super-intelligence right now is like worrying about overpopulation on Mars. Not that it might not eventually be a serious concern, but that we will get a higher return investing our intellectual efforts right now on more immediate problems.
The standard counter to this is that super-intelligence might always seem like it is well beyond our current capabilities -- maybe centuries in the future -- until, all of a sudden, it appears as the result of an uncontrollable chain reaction known as an "intelligence explosion", or "singularity". (As far as I can tell, very few people actually think that intelligence growth would exhibit an actual mathematical singularity --- this seems instead to be a metaphor for exponential growth.) If this is what we expect, then now might very well be the time to worry about super-intelligence. The first argument of this form was put forth by British mathematician I.J. Good (of
Good-Turing Frequency Estimation!):
“Let an ultraintelligent machine be defined as a machine that can far surpass all the intellectual activities of any man however clever. Since the design of machines is one of these intellectual activities, an ultraintelligent machine could design even better machines; there would then unquestionably be an ‘intelligence explosion,’ and the intelligence of man would be left far behind. Thus the first ultraintelligent machine is the last invention that man need ever make, provided that the machine is docile enough to tell us how to keep it under control.”
Scott Alexander summarizes the same argument a bit more quantitatively. In this passage, he is imagining the starting point being a full-brain simulation of Einstein --- except run on faster hardware, so that our simulated Einstein operates at a much faster clock-speed than his historical namesake:
It might, like the historical Einstein, contemplate physics. Or it might contemplate an area very relevant to its own interests: artificial intelligence. In that case, instead of making a revolutionary physics breakthrough every few hours, it will make a revolutionary AI breakthrough every few hours. Each AI breakthrough it makes, it will have the opportunity to reprogram itself to take advantage of its discovery, becoming more intelligent, thus speeding up its breakthroughs further. The cycle will stop only when it reaches some physical limit – some technical challenge to further improvements that even an entity far smarter than Einstein cannot discover a way around.
To human programmers, such a cycle would look like a “critical mass”. Before the critical level, any AI advance delivers only modest benefits. But any tiny improvement that pushes an AI above the critical level would result in a feedback loop of inexorable self-improvement all the way up to some stratospheric limit of possible computing power.
This feedback loop would be exponential; relatively slow in the beginning, but blindingly fast as it approaches an asymptote. Consider the AI which starts off making forty breakthroughs per year – one every nine days. Now suppose it gains on average a 10% speed improvement with each breakthrough. It starts on January 1. Its first breakthrough comes January 10 or so. Its second comes a little faster, January 18. Its third is a little faster still, January 25. By the beginning of February, it’s sped up to producing one breakthrough every seven days, more or less. By the beginning of March, it’s making about one breakthrough every three days or so. But by March 20, it’s up to one breakthrough a day. By late on the night of March 29, it’s making a breakthrough every second.
As far as I can tell, this possibility of an exponentially-paced intelligence explosion is the main argument for folks devoting time to worrying about super-intelligent AI
now, even though current technology doesn't give us anything even close. So in the rest of this post, I want to push a little bit on the claim that the feedback loop induced by a self-improving AI would lead to exponential growth, and see what assumptions underlie it.
A Toy Model for Rates of Self Improvement
Lets write down an extremely simple toy model for how quickly the intelligence of a self improving system would grow, as a function of time. And I want to emphasize that the model I will propose is clearly a toy: it abstracts away everything that is interesting about the problem of designing an AI. But it should be sufficient to focus on a simple question of asymptotics, and the degree to which growth rates depend on the extent to which AI research exhibits diminishing marginal returns on investment. In the model, AI research accumulates with time: at time t, R(t) units of AI research have been conducted. Perhaps think of this as a quantification of the number of AI "breakthroughs" that have been made in Scott Alexander's telling of the intelligence explosion argument. The intelligence of the system at time t, denoted I(t), will be some function of the accumulated research R(t). The model will make two assumptions:
- The rate at which research is conducted is directly proportional to the current intelligence of the system. We can think about this either as a discrete dynamics, or as a differential equation. In the discrete case, we have: $R(t+1) = R(t) + I(t)$, and in the continuous case: $\frac{dR}{dt} = I(t)$.
- The relationship between the current intelligence of the system and the currently accumulated quantity of research is governed by some function f: $I(t) = f(R(t))$.
The function f can be thought of as capturing the marginal rate of return of additional research on the actual intelligence of an AI. For example, if we think AI research is something like pumping water from a well --- a task for which doubling the work doubles the return --- then, we would model f as linear: $f(x) = x$. In this case, AI research does not exhibit any diminishing marginal returns: a unit of research gives us just as much benefit in terms of increased intelligence, no matter how much we already understand about intelligence. On the other hand, if we think that AI research should exhibit diminishing marginal returns --- as many creative endeavors seem to --- then we would model f as an increasing concave function. For example, we might let $f(x) = \sqrt{x}$, or $f(x) = x^{2/3}$, or $f(x) = x^{1/3}$, etc. If we are really pessimistic about the difficulty of AI, we might even model $f(x) = \log(x)$. In these cases, intelligence is still increasing in research effort, but the rate of increase as a function of research effort is diminishing, as we understand more and more about AI. Note however that the rate at which research is being conducted is increasing, which might still lead us to exponential growth in intelligence, if it increases fast enough.
So how does our choice of f affect intelligence growth rates? First, lets consider the case in which $f(x) = x$ --- the case of no diminishing marginal returns on research investment. Here is a plot of the growth over 1000 time steps in the discrete model:
Here, we see exponential growth in intelligence. (It isn't hard to directly work out that in this case, in the discrete model, we have $I(t) = 2^t$, and in the continuous model, we have $I(t) = e^t$). And the plot illustrates the argument for worrying about AI risk now. Viewed at this scale, progress in AI appears to plod along at unimpressive levels before suddenly shooting up to an unimaginable level: in this case, a quantity if written down as a decimal that would have more than 300 zeros.
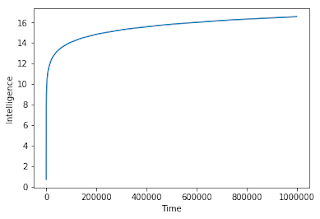
It isn't surprising that if we were to model severely diminishing returns --- say $f(x) = \log(x)$, that this would not occur. Below, we plot what happens when $f(x) = \log(x)$, with time taken out all the way to 1,000,000 rather than merely 1000 as in the above plot:
Intelligence growth is not very impressive here. At time 1,000,000 we haven't even reached 17. If you wanted to reach (say) an intelligence level of 30 you'd have to wait an unimaginably long time. In this case, we definitely don't need to worry about an "intelligence explosion", and probably not even about ever reaching anything that could be called a super-intelligence.
But what about moderate (polynomial) levels of diminishing marginal returns. What if we take $f(x) = x^{1/3}$? Lets see:
Ok --- now we are making more progress, but even though intelligence now has a polynomial relationship to research (and research speed is increasing, in a chain reaction!) the rate of growth in intelligence is still decreasing. What about if $f(x) = \sqrt{x}$? Lets see:
At least now the rate of growth doesn't seem to be decreasing: but it is growing only linearly with time. Hardly an explosion. Maybe we just need to get more aggressive in our modeling. What if $f(x) = x^{2/3}$?
Ok, now we've got something! At least now the rate of intelligence gains is increasing with time. But it is increasing more slowly than a quadratic function -- a far cry from the exponential growth that characterizes an intelligence explosion.
Lets take a break from all of this plotting. The model we wrote down is simple enough that we can just go and solve the differential equation. Suppose we have $f(x) = x^{1-\epsilon}$ for some $\epsilon > 0$. Then the differential equation solves to give us:
\[I(t) = \left(\left(1+\epsilon t \right)^{1/\epsilon} \right)^{1-\epsilon} \]
What this means is that for any positive value of $\epsilon$, in this model, intelligence grows at only a polynomial rate. The only way this model gives us exponential growth is if we take $\epsilon \rightarrow 0$, and insist that $f(x) = x$ --- i.e. that the intelligence design problem does not exhibit any diminishing marginal returns at all.
Thoughts
So what do we learn from this exercise? Of course one can quibble with the details of the model, and one can believe different things about what form for the function f best approximates reality. But for me, this model helps crystallize the extent to which the "exponential intelligence explosion" story crucially relies on intelligence design being one of those rare tasks that doesn't exhibit any decreasing marginal returns on effort at all. This seems unlikely to me, and
counter to experience.
Of course, there
are technological processes out there that do appear to exhibit exponential growth, at least for a little while.
Moore's law is the most salient example. But it is important to remember that even exponential growth for a little while need not
seem explosive at human time scales. Doubling every day corresponds to exponential growth, but so does increasing by 1% a year. To
paraphrase Ed Felten: our retirement plans extend beyond depositing a few dollars into a savings account, and waiting for the inevitable "wealth explosion" that will make us unimaginably rich.
Postscript
I don't claim that anything in this post is either novel or surprising to folks who spend their time thinking about this sort of thing. There is at least
one paper that writes down a model including diminishing marginal returns, which yields a linear rate of intelligence growth.
It is also interesting to note that in the model we wrote down, exponential growth is really a knife edge phenomenon. We already observed that we get exponential growth if $f(x) = x$, but not if $f(x) = x^{1-\epsilon}$ for any $\epsilon > 0$. But what if we have $f(x) = x^{1+\epsilon}$ for $\epsilon > 0$? In that case, we don't get exponential growth either! As Hadi Elzayn pointed out to me,
Osgood's Test tell us that in this case, the function $I(t)$ contains an actual mathematical singularity --- it approaches an infinite value in finite time.